As frequências, ou proporções, ideias alélicas e genotípicas
numa população são definidas pela Lei de Hardy-Weinberg, também chamada de Lei
do Equilíbrio (na área de ecologia).
A equação determina que a frequência alélica seja o valor
obtido por:
Número de cópias do alelo na população/ número de cópias
desses genes na população.
Vamos brincar com um exemplo:
Imagine um gene para os alelos "A" e "a" numa população de lobos.
Há três genótipos possíveis: AA, Aa e aa. Com um estudo de
marcadores numa amostra da população, você descobriu que há 36 indivíduos AA,
48 Aa e 16 aa. Se somar a quantidade de indivíduos, pode-se
contar 100. Última coisa a se fazer para se saber a frequência genotípica observada
é a divisão. 48/ 100= 0,48 (AA);36/ 100= 0,36 (Aa) e 16/100= 0,16 (aa). É
importante comentar que a soma das frequências genotípicas têm de dar 1 e
qualquer valor diferente indica alguma coisa errada nos cálculos.
As frequências alélicas também são mensuradas através dessa
amostragem de marcadores. Por exemplo: A quantidade de alelos A para os 48 indivíduos
AA é 96 (48 do primeiro A e 48 do segundo A para todos esses indivíduos), para
os 36 Aa é 36 (36 direto da metade do genótipo desses indivíduos) e nenhum para
os 16 aa, finalizando em 132 alelos A na população. Seguindo o mesmo raciocínio,
encontra-se 68 alelos a. Vamos lembrar que são 100 indivíduos nessa população e
cada tem 2 alelos em seus genótipos, totalizando 200 alelos desse gene nessa
população. Se dividirmos 132/200 e 68/200, conseguimos os valores das
frequências alélicas para A (0,66) e a (0,34).
A Lei do Equilíbrio é utópica e não real. Ah então tudo isso
que vi foi inútil?! Tenha calma... Essa regra determina como visto acima,
proporções ideais. Essa utopia é para populações muito grandes (que não ocorrem
no meio natural por questões de sobrevivência), sem seleção natural ou sexual e
até mesmo sem mutação. Entretanto,
sabemos que essas coisas ocorrem no ambiente natural. Para compreender a
aplicação desses cálculos, precisamos transformar as frequências alélicas em
probabilidades p=A e q (1-p)= a.
Agora voltamos a nosso exemplo. O ideal de proporção genotípica
é finalmente encontrado por mais um cálculo (mais um?!). Se A= 0,66 e a= 0,34,
temos que a porcentagem de indivíduos AA para esse gene numa população ideal é
de 0,66 x 0,66 = 0,4356 ou seja 43,56%; 44,88 % de Aa (2 x 0,66 x 0,34= 0,4488)
e 11,56 % de aa ( 0,34 x 0,34= 0,1156). Se somarmos as porcentagens encontramos
100 % e qualquer valor diferente indica, meu querido amiguinho, um erro de
cálculo.
Como visto acima, a Lei de Hardy-Weinberg está relacionada a
um ambiente utópico, com seleção sexual aleatória. Isso não ocorre em população
alguma.
Fonte: Butterflies of America
Borboletas Morpho selecionam seus pares pelo território,
onde os entomólogos percebem que os machos são territoriais e agressivos,
inclusive com roupas de cetim azuladas (pois é, eles voarão em tua direção se
for com uma roupa assim na floresta). Nesse caso os genes ligados a
metabolismos mais rápidos são os que mais persistem na população.
Chega de exemplos... Pode acontecer de essa seleção sexual
gerar endocruzamento e um indivíduo aa fazer par com outro aa, e
consequentemente, alterando a Lei do Equilíbrio e diminuindo o número de
heterozigotos. Quando semelhantes se reproduzem diz-se acasalamento seletivo
positivo e quando diferentes diz-se negativo.
Essa Lei , quando alterada, indica que está havendo
endocruzamento numa população. Como?
Há outra fórmula (juro que é a última de hoje) que define o
coeficiente de endocruzamento.
Onde:
F= coeficiente de endocruzamento.
H.hwe= frequência genotípica de heterozigotos ideal.
H.obs= frequência genotípica de heterozigotos observada.
Em nossa população de lobos estudada, a frequência ideal de
heterozigotos é de 0,4488. Tu decides fazer coleta , sei lá, no ano seguinte e
mensurando, via marcadores gênicos, descobre uma frequência genotípica de
heterozigotos observada de 0,2244, no ano depois 0,8976 e por fim 0,3366.
Ano 0=
Ano 1= F= 0,4488 - 0,2244/ 0,4488= 0,5.
Ano 2= F= 0,4488 - 0,8976/ 0,4488= -1
Ano 3= F= 0,4488- 0,3366/ 0,4488= 0,25.
Valores de coeficiente para os anos.
Em outras palavras, quanto mais heterozigotos observados,
menor será o coeficiente e vice-versa. Nos anos 1 e 3 (principalmente 1) há
maior risco de que genes deletérios, compartilhados pelos homozigotos causem
dano a população, gerando a depressão por endocruzamento.
Nossa população de lobinhos no gráfico.
Quando a reprodução ocorre entre primos os valores de
coeficiente de endocruzamento indicam 0,125, entre irmãos, de 0,25 e
autocruzamento é de 0,5. Em nossa brincadeira, a população teve muitos
autocruzamentos no Ano 1 e relacionamento entre primos no Ano 3. Esses valores
sozinhos não dizem muito, mas, quando juntos de uma avaliação por
bioindicadores, pode me dizer, por exemplo, se está havendo fragmentação de
habitat e mais reproduções entre semelhantes ou se esta dispersando e mais
entre diferentes.
Apesar disso tudo, o endocruzamento não é o único fator
associado a perda de variabilidade. Veremos a seguir, a que forças invencíveis uma
população está vulnerável em meio natural.
Referências:
RICKLEFS, R.E. 2010. A Economia da Natureza. 6ª ed. Editora Guanabara Koogan, Rio de Janeiro.


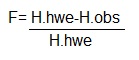












0 comentários:
Postar um comentário